分散分析(F検定)
対ではない異なる標本間の平均値の差を検定するにあたり、等分散を仮定できるかどうかで検定方法が異なるため、t検定の前にF検定を実施します。
2つのグループの分散が等しいことを帰無仮説として検定を行ないます。
帰無仮説(H0):分散が等しい
対立仮説(H1):分散が等しくない
※コツ
・分散比が1より大きくなるようにする。1つ目の変数に分散の大きいものを持ってきます。
・2つのグループの標本数は異なっていても構いません。
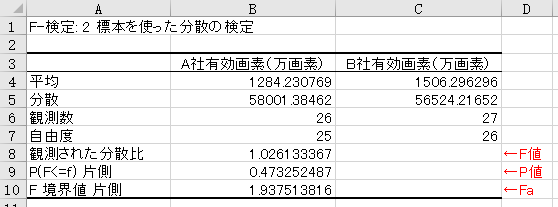
この例では、P値が事前に設定した0.05よりも大きいこと、またF境界値(Fa)が分散比(F値)よりも大きいことから、
帰無仮説を棄却できない
| P値 |
事前に設定した棄却域の確率(0.05等)より小さければ帰無仮説を棄却できる(分散に差がある) 事前に設定した棄却域の確率(0.05等)より大きければ帰無仮説を棄却できない(等分散) |
|
F境界値 |
F値より小さければ帰無仮説を棄却できる(分散に差がある) 頭でっかち F値より大きければ帰無仮説を棄却できない(等分散) 雪だるま |
【解説】
2群の分散が等しい,という仮説が正しいことを前提とした場合,観測された分散比は既に知られている確率分布に従います。
標本から得られた1.02という数値とサンプル数から計算されるp値0.47は,この既に知られている確率分布のもとで,標本から観測された分散比がどの程度の確率で観測されるかを示しています。0.47ですので,47%の確率で観測される数値であるということです。
この数値が,分析者が決めた水準,一般的には1%あるいは5%以下である場合,非常に稀な事象が標本において検出されていることになります。それを根拠として,そもそも前提とした帰無仮説が間違いであるという結論を導きます。これにより帰無仮説はp値が0.01もしくは0.05以下である場合,棄却されます。
