t検定
t検定・・・平均値を比較する たまたまか? 意味のある違いか?

「対応のあるデータ」・・・一対の標本(対象が同じ、事の前後で比較)
「対応のないデータ」・・・F検定の結果、いずれかの検定方法をとる
├─等分散と仮定した2標本による検定
└─分散が等しくないと仮定した2標本による検定
F検定の結果
P(F<=f)片側 に注目する
└これを2倍して両側にする。
├─0.05より大きい = 分散が等しい
└─0.05より小さい = 分散が等しくない
t検定の結果
P(T<=t)両側 に注目する
├─0.05より大きい = 意味のあるさとは言い切れない
└─0.05より小さい = 意味のある差
2つの変数間で平均の差が設定した0などであるという帰無仮説を検定します。
帰無仮説(H0):平均の差はない(0である)
対立仮説(H1):平均に差はある
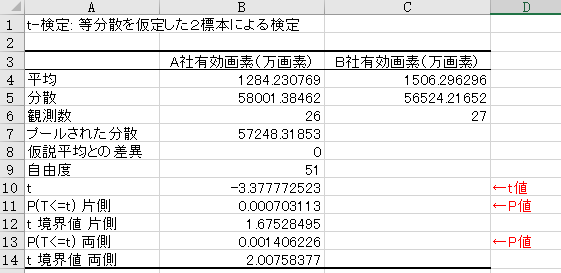
この例では、P値が設定した0.05よりもはるかに小さく、
またt値の絶対値はt境界値よりも大きいことから
統計的に高い有意性をもって2変数の平均値の差が0とは言えないことを示しています。
|
P値 < 棄却域の確率(0.05など) P値 > 棄却域の確率(0.05など) |
帰無仮説を棄却(平均に差はある) 帰無仮説を棄却できない(平均に差はない) |
|
t境界値 < t値の絶対値 頭でっかち型 t境界値 > t値の絶対値 雪だるま型 |
帰無仮説を棄却(平均に差はある) 帰無仮説を棄却できない(平均に差はない) |
