確率・事象・組合せ
<用語>
◆確率 ・・・ 不確かな事象の起こりやすさの程度を表す数値
◆同様に確からしい ・・・ コインの表裏のように起こる可能性が等しい状況
◆無作為 ・・・ 同様に確からしく事象を起こす手順
◆オッズ ・・・ 起きる確率 ÷ 起きない確率 p/(1-p)
失敗b回に対して成功a回の割合のときに、a/bの値
◆試行 ・・・ 結果が偶然に支配される実験
<ルール>
確率変数は、大文字
実現値 は、小文字
^P など 「^」は推定値
事象
◆基本事象
2つのサイコロを投げる例では36通りの結果がある。これらの事象はこれ以上分解できないため、基本事象と呼ばれる。
◆複数事象の組み合わせ
- 和事象・・・A∪B (AまたはB)
- 積事象・・・A⋂B (AかつB)
-
余事象・・・̅A (Aが起きない)
- 空事象・・・φ={} 、 φ=⁻Ω
- 排反・・・A⋂B=φ (AとBが同時に起こりえない。AとBは単独で起こる)

※思考力を鍛える数学 さんより
◆事象の独立性
2つの事象において、片方の事象が起こるか否かがもう片方の事象が起こる確率に影響を与えないこと。具体的には、下記の式が成り立つとき、AとBは独立である。
P(A⋂B)=P(A)・P(B)
標本空間
◆集合・・・一定の条件を満たす集まり。 大文字A,Bなどで表す。
◆要素・・・集合を構成する個々のもの。 小文字a,bなどで表す。 a A
◆全事象(標本空間)・・・Ωで表す。 サイコロの目 Ω={e1,e2,e3,e4,e5,e6}
確率
◆公理
- 確率は常に+(プラス)の値である。非負。 0 ≦ P(A) ≦ 1
- 全事象Ωの確率は1である。 P(Ω)=1 P(φ)=0
- 排反事象の加法定理 P(A∪B) = P(A)+P(B)
◆定理
- 事象Aが起こらない確率は1-A P(Ā)=1―P(A)、P(A)=1―P(Ā) A∪Ā = Ω
- Aが起きれば必ずBが起きる(A⊂B)ならば、P(A)≦P(B)
- ABの少なくともいずれかが起こる確率は P(A∪B)=P(A)+P(B)-P(A⋂B)
※重なった部分を二重カウントしないように - A、Bが排反ならば P(A∪B)=P(A)+P(B)
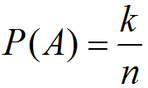
◆事象Aの起こる確率の定義
<条件>
- 起こりうる場合の数がn通り
- 事象Aが起こりうる場合の数がk通り
- 同様に確からしいとき

◆条件付き確率
事象Aが与えられた時の事象Bの条件付き確率P(B|A)は右のようになる。
例)日本全国から1名を無作為に選ぶ場合、男性である確率は約1/2であるが、もし選ばれた人が自衛官であることが分かっている場合は、男性である確率が高くなることが予想される。このようにある条件を付けた時の確率を条件付き確率という。

◆反復試行の確率
1回の試行で事象Aが起こる確率をPとした場合、
同じ試行をn回独立に繰り返したとき、
事象Aがk回起こる確率はこのようになる。
例)サイコロを5回投げて、6の目がちょうど3回でる確率。
(場合の数)×(それが起こる確率)×(それが起こらない確率)
順列・組合せ
何通りの組合せパターンがあるかを確認する方法

◆順列 (1枚ずつ順番に抜き出すとき)
n枚のカードから1枚ずつ順番にk枚を抜き出すと何通りの結果があり得るかを右の式で求められる。
※試行の回数分だけ項を乗じる。
10・9・8・7・6・5・4・3・2・1
4回試行したら↑ここまで乗じる。

すべてを抜き出す場合は、nの階乗となる。
◆組合せ (まとめて抜き出すとき)
n枚のカードからまとめて1度にk枚を抜き出すと何通りの結果があり得るかを下記の式で求められる。
※試行の回数がキーとなる。
10・9・8・7・6・5・4・3・2・1
n=10で4回試行したとすると赤文字が分子 青文字が分母。

5C5 や 5C0 のように極端なものは、計算せずとも1
5C4 や 5C1 のように極端から1つ歩み寄ったものは、計算せずともn (この場合5)
